PROBABLIDAD
La probabilidad es una medida de la certidumbre de que ocurra un evento. Su valor es un número entre 0 y 1, donde un evento imposible corresponde a cero y uno seguro corresponde a uno.
Una forma empírica de estimar la probabilidad consiste en obtener la frecuencia con la que sucede un determinado acontecimiento mediante la repetición de experimentos aleatorios, bajo condiciones suficientemente estables. En algunos experimentos de los que se conocen todos los resultados posibles, la probabilidad de estos sucesos pueden ser calculadas de manera teórica, especialmente cuando todos son igualmente probables.
La teoría de la probabilidad es la rama de la matemática que estudia los experimentos o fenómenos aleatorios. Se usa extensamente en áreas como la estadística, la física, las ciencias sociales, la Investigación médica, las finanzas, la economía y la filosofía para conocer la viabilidad de sucesos y la mecánica subyacente de sistemas complejos.
TECNICA DE CONTEO
Las técnicas de conteo son estrategias matemáticas usadas en probabilidad y estadística que permiten determinar el número total de resultados que pueden haber a partir de hacer combinaciones dentro de un conjunto o conjuntos de objetos. Este tipo de técnicas se utilizan cuando es prácticamente imposible o demasiado pesado hacer de forma manual combinaciones de diferentes elementos y saber cuántas de ellas son posibles.
Este concepto se entenderá de forma más sencilla a través de un ejemplo. Si se tienen cuatro sillas, una amarilla, una roja, una azul y una verde, ¿cuántas combinaciones de tres de ellas se pueden hacer ordenadas una al lado de la otra?
Se podría resolver a este problema haciéndolo manualmente, pensando en combinaciones como azul, rojo y amarillo; azul, amarillo y rojo; rojo, azul y amarillo, rojo, amarillo y azul… Pero esto puede requerir mucha paciencia y tiempo, y para eso haríamos uso de las técnicas de conteo, siendo para este caso necesaria una permutación.
NUMEROS FACTORIALES
La función factorial se representa con un signo de exclamación “!” detrás de un número. Esta exclamación quiere decir que hay que multiplicar todos los números enteros positivos que hay entre ese número y el 1.
Por ejemplo:
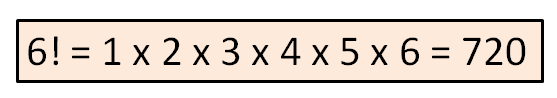
A este número, 6! le llamamos generalmente “6 factorial”, aunque también es correcto decir “factorial de 6”.
En tu calculadora podrás ver una tecla con “n!” o “x!”. Esta tecla te servirá para calcular directamente el factorial del número que quieras.
PERMUTACIONES
Las permutaciones son agrupaciones en las que importa el orden de los objetos. Las combinaciones son agrupaciones en las que el contenido importa pero el orden no. Dos eventos son dependientes si el estado original de la situación cambia de un evento al otro, y esto altera la probabilidad del segundo evento.
a) No se permite repeticiones de elementos
b) si se permite repetición de elementos
nPr= nr
COMBINACIONES
Es un arreglo ordenado de elementos en donde no importa; al igual que con las permutaciones tenemos dos casos que son los siguientes:
a) Si se permite combinaciones
b) No se permite combinaciones
CONCLUSION: En este espacio te enseñan las combinaciones por ejemplo si quieres saber cuantas combinaciones hay, son dos métodos el primero es un diagrama poniendo cada articulo con el contrario, o una mas fácil multiplicarlos.
Aquí te dejo un video para mayor comprensión



No hay comentarios.:
Publicar un comentario