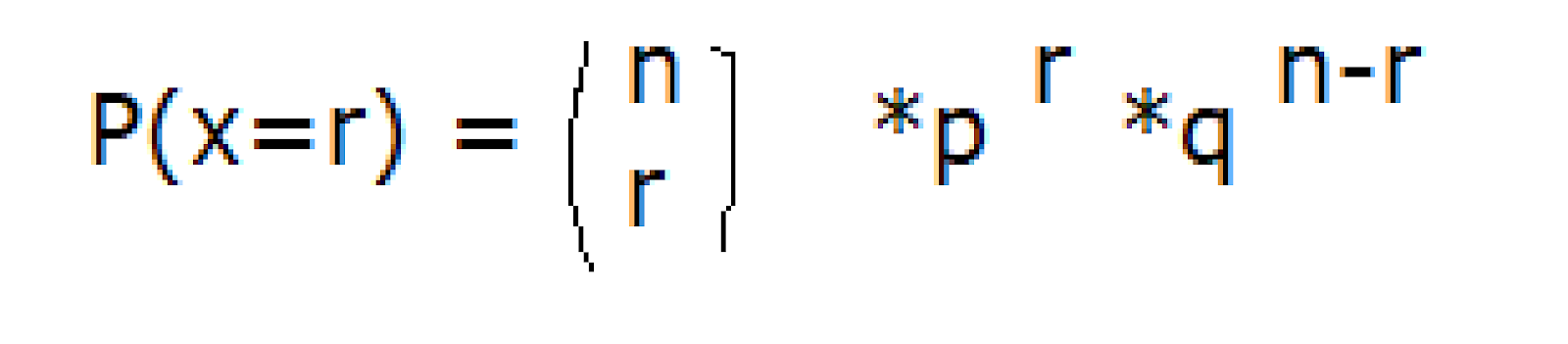DISTRIBUCIONES CONTINUAS

 DISTRIBUCION NORMAL 

La distribución normal es la más importante de todas las distribuciones de probabilidad. Es una distribución de variable continua con campo de variación [-¥ ,¥ ], que queda especificada a través de dos parámetros ( que acaban siendo la media y la desviación típica de la distribución).

Una variable aleatoria continua, X, definida en [-¥ ,¥ ] seguirá una distribución normal de parámetros m y s , ( X ~ N(m ; s ) ) , si su función de densidad es :

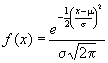 para x Î [-¥ ,¥ ]

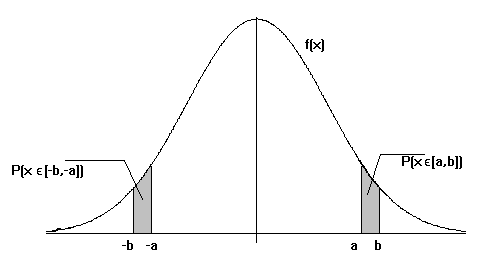
cuya representación gráfica es:

Importancia de la distribución Normal.

a) Enorme número de fenómenos que puede modelizar: Casi todas las características cuantitativas de las poblaciones muy grades tienden a aproximar su distribución a una distribución normal.

b) Muchas de las demás distribuciones de uso frecuente, tienden a distribuirse según una Normal, bajo ciertas condiciones.

c) (En virtud del teorema central del límite).Todas aquellas variables que pueden considerarse causadas por un gran número de pequeños efectos (como pueden ser los errores de medida) tienden a distribuirse según una distribución normal.

La probabilidad de cualquier intervalo se calcularía integrando la función de densidad a lo largo de ese de intervalo, pero no es necesario nunca resolver la integral pues existen tablas que nos evitan este problema.

F.G.M.: puede probarse que la función generatriz de momentos de una distribución N(m ; s ) es:

                                                                        f (t) = E(e^tx) = e(^{m t + ½ s2t2})

A partir de ella es fácil comprobar como efectivamente la media de la distribución es el parámetro m y, cómo su varianza es el parámetro s .

Igualmente puede comprobarse que la distribución es simétrica y que su curtósis es nula.

Propiedad importante: "CUALQUIER TRANSFORMACIÓN LINEAL DE UNA VARIABLE ALEATORIA NORMAL TIENE TAMBIÉN UNA DISTRIBUCIÓN NORMAL DONDE LA MEDIA DE LA NUEVA VARIABLE ES LA MISMA TRANSFORMACIÓN LINEAL DE LA MEDIA DE LA ANTIGUA Y DONDE LA DESVIACIÓN TÍPICA ES LA DESVIACIÓN TÍPICA ANTIGUA MULTIPLICADA POR EL COEFICIENTE ANGULAR DE LA TRANSFORMACIÓN":

Dada una variable X ~ N(m ; s ) si la nueva variable Y es Y = a+bX

Y~ N(a+bm ; bs ) :

en efecto: la F.G.M de la distribución de X será:

E(e^tx) = e(^{m t + ½ s2t2})

y la F.G.M. de la distribución de Y será:

fy(t)= e^at.f_x(bt) = e^at .e(^{m bt + ½ s2b2t2}) = e(^(a+bm )t + (bs )²t²)

que es la F.G.M de una distribución N(a+bm ; bs ) //*q.e.d.*//

Consecuencia importante de esto es que si se tipifica una variable X / X ~ N(m ; s ) la nueva variable Z = tendrá una distribución N(0,1).

La distribución N(0,1) se conoce con el nombre de Normal tipificada o reducida y tiene una importancia teórica y práctica fundamental.Su Función de distribución está tabulada y ello nos permite calcular directamente cualquier probabilidad de cualquier intervalo de cualquier distribución normal ( X ~ N(m ; s )), sin necesidad de integrar.

En efecto: si X ~ N(m ; s ) y queremos calcular P(XΠ[a,b])==P(a£ X £ b) =

donde F es la F. de distribución de una Normal tipificada, que puede evaluarse a través de las tablas.

DISTRIBUCION UNIFORME: 

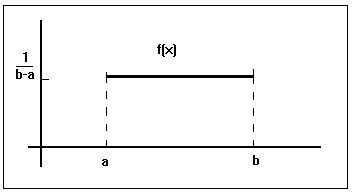
 La distribución o modelo uniforme puede considerarse como proveniente de un proceso de extracción aleatoria .El planteamiento radica en el hecho de que la probabilidad se distribuye uniformemente a lo largo de un intervalo . Así : dada una variable aleatoria continua, x , definida en el intervalo [a,b] de la recta real, diremos que x tiene una distribución uniforme en el intervalo [a,b] cuando su función de densidad para  sea:  para x Î [a,b].

Su representación gráfica será :

De manera que la función de distribución resultará:

Su representación gráfica será :

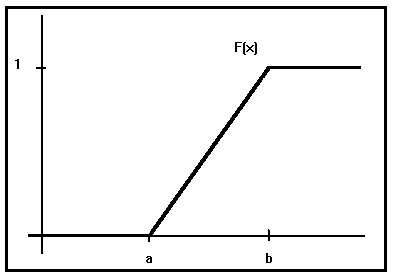
Este modelo tiene la característica siguiente : Si calculamos la probabilidad del suceso
                                                                        

                                Tendremos: 

                Este resultado nos lleva a la conclusión de que la probabilidad de cualquier suceso depende únicamente de la amplitud del intervalo (D X) , y no de su posición en la recta real [a , b] . Lo que viene ha demostrar el reparto uniforme de la probabilidad a lo largo de todo el campo de actuación de la variable , lo que , por otra parte, caracteriza al modelo.

En cuanto a las ratios de la distribución tendremos que la media tiene la expresión:

La varianza tendrá la siguiente expresión:

                                                de donde 

                                        por lo que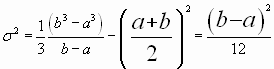 

La función generatriz de momentos vendrá dada por :

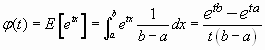
Lógicamente partiendo de esta función podríamos recalcular media y varianza gracias al teorema de los momentos

DISTRIBUCION EXPONENCIAL 

 A pesar de la sencillez analítica de sus funciones de definición, la distribución exponencial tiene una gran utilidad práctica ya que podemos considerarla como un modelo adecuado para la distribución de probabilidad del tiempo de espera entre dos hechos que sigan un proceso de Poisson. De hecho la distribución exponencial puede derivarse de un proceso experimental de Poisson con las mismas características que las que enunciábamos al estudiar la distribución de Poisson, pero tomando como variable aleatoria , en este caso, el tiempo que tarda en producirse un hecho

Obviamente, entonces , la variable aleatoria será continua. Por otro lado existe una relación entre el parámetro a de la distribución exponencial , que más tarde aparecerá , y el parámetro de intensidad del proceso l , esta relación es a = l

Al ser un modelo adecuado para estas situaciones tiene una gran utilidad en los siguientes casos:

· Distribución del tiempo de espera entre sucesos de un proceso de Poisson

· Distribución del tiempo que transcurre hasta que se produce un fallo, si se cumple la condición que la probabilidad de producirse un fallo en un instante no depende del tiempo transcurrido .Aplicaciones en fiabilidad y teoría de la supervivencia.

Función de densidad.

    A pesar de lo dicho sobre que la distribución exponencial puede derivarse de un proceso de Poisson , vamos a definirla a partir de la especificación de su función. de densidad:

    Dada una variable aleatoria X que tome valores reales no negativos {x ³ 0} diremos que tiene una distribución exponencial de parámetro a con a ³ 0, si y sólo si su función de densidad tiene la expresión: 

                                                                        Diremos entonces que 

 

 

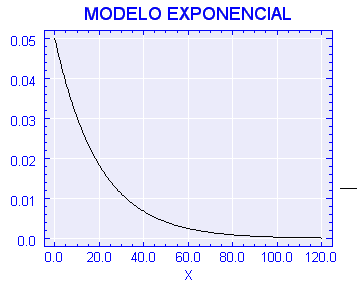
Gráficamente como ejemplo planteamos el modelo con parámetro a =0,05

 

 

 

 

                                    En consecuencia , la función de distribución será:

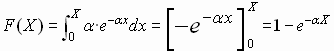
    En la principal aplicación de esta distribución , que es la Teoría de la Fiabilidad, resulta más interesante que la función de distribución la llamada Función de Supervivencia o Función de Fiabilidad.

                La función de Supervivencia se define cómo la probabilidad de que la variable aleatoria tome valores superiores al valor dado X:

        Si el significado de la variable aleatoria es "el tiempo que transcurre hasta que se produce el fallo": la función de distribución será la probabilidad de que el fallo ocurra antes o en el instante X: y , en consecuencia la función de supervivencia será la probabilidad de que el fallo ocurra después de transcurrido el tiempo X ; por lo tanto, será la probabilidad de que el elemento, la pieza o el ser considerado "Sobreviva" al tiempo X ; de ahí el nombre.

Gráficamente, la función de distribución para un modelo exponencial de parámetro a =0,05 sería :

 

 

 

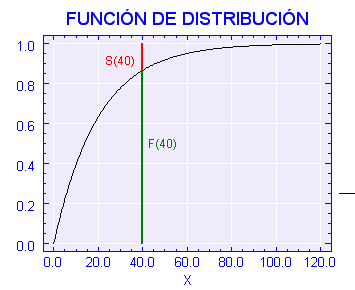
En la que se observa lo que sería la diferencia entre función de distribución y la de supervivencia

 

 

 

 

                La Función Generatriz de Momentos será :

                                                    

                             

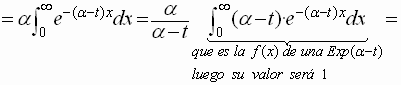
                                      tendremos así que la F.G.M será :

                                                                                      

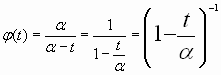
    Una vez calculada la F.G.M podemos , partiendo de ella , calcular la media y la varianza

                Así la media será:

               En cuando a la varianza su expresión será :

 ya que

        La mediana del modelo exponencial será aquel valor de la variable x =Me que verifica que F(Me) = ½

                            De manera que  por lo que 

 

Tasa instantánea de fallo.

    Dentro del marco de la teoría de la fiabilidad si un elemento tiene una distribución del tiempo para un fallo con una función de densidad f(x) , siendo x la variable tiempo para que se produzca un fallo , y con una función de supervivencia S(X) La probabilidad de que un superviviente en el instante t falle en un instante posterior t + D t será una probabilidad condicionada que vendrá dada por:

    Al cociente entre esta probabilidad condicionada y la amplitud del intervalo considerado, t , se le llama tasa media de fallo en el intervalo [t , t+D t] :

Y a la tasa media de fallo en un intervalo infinitésimo es decir, al límite de la tasa media de fallo cuando D t® 0 se le llama Tasa Instantánea de Fallo (o, simplemente, tasa de fallo) en t:

            La tasa de fallo es, en general, una función del tiempo, que define unívocamente la distribución.

        Pues bien, puede probarse que el hecho de que la tasa de fallo sea constante es condición necesaria y suficiente para que la distribución sea exponencial y que el parámetro es, además, el valor constante de la tasa de fallo.

en efecto:

                                si 

                 de donde  integrando esta ecuación diferencial entre 0 y x :

                                    

                             de modo que la función de distribución será

                                                          Función de Distribución de una Exponencial

                    Si X tiene una distribución exponencial 

                                                    de manera que 

        Así pues si un elemento tiene una distribución de fallos exponencial su tasa de fallos se mantiene constante a lo largo de toda la vida del elemento. La probabilidad de fallar en un instante no depende del momento de la vida del elemento en el que nos encontremos; lo que constituye la propiedad fundamental de la distribución que ahora enunciamos:

Propiedad fundamental de la distribución exponencial

La distribución exponencial no tiene memoria :

    Poseer información de que el elemento que consideramos ha sobrevivido un tiempo S (hasta el momento) no modifica la probabilidad de que sobreviva t unidades de tiempo más. La probabilidad de que el elemento falle en una hora (o en un día, o en segundo) no depende del tiempo que lleve funcionando. No existen envejecimiento ni mayor probabilidad de fallos al principio del funcionamiento

       Expresión que no depende , como se observa , del tiempo sobrevivido s.

CONCLUSION: Con esto podemos concluir que estas tres distribuciones describe las probabilidades de los posibles valores de una variable aleatoria continua. Una variable aleatoria continua es una variable aleatoria con un conjunto de valores posibles (conocido como el rango) que es infinito y no se puede contar.

 AQUI TE DEJO UN VIDEO 

PARA MEJOR COMPRENSION: 

Distribución de probabilidad

 Distribución uniforme discreta

En teoría de probabilidad y estadística, la distribución uniforme discreta es una distribución de probabilidad discreta simétrica que surge en espacios de probabilidad equiprobables, es decir, en situaciones donde de ${\displaystyle n}$ resultados diferentes, todos tienen la misma probabilidad de ocurrir.

Un ejemplo simple de la distribución uniforme discreta es tirar los dados. Los valores posibles son 1, 2, 3, 4, 5, 6 y cada vez que se lanza el dado, la probabilidad de una puntuación determinada es de 1/6. Si se lanzan dos dados y se suman sus valores, la distribución resultante ya no es uniforme porque no todas las sumas tienen la misma probabilidad. Aunque es conveniente describir distribuciones uniformes discretas sobre enteros, como este, también se pueden considerar distribuciones uniformes discretas sobre cualquier conjunto finito . Por ejemplo, una permutación aleatoria es una permutación generada uniformemente a partir de las permutaciones de una longitud determinada, y un árbol de expansión uniforme es un árbol de expansión. generado uniformemente a partir de los árboles de expansión de un gráfico dado.

La distribución uniforme discreta en sí misma es intrínsecamente no paramétrica. Es conveniente, sin embargo, para representar sus valores en general por todos los números enteros en un intervalo [ a , b ], de modo que una y b se convierten en los principales parámetros de la distribución (a menudo uno simplemente considera el intervalo [1, n ] con la sola parámetro n ). Con estas convenciones, la función de distribución acumulativa (CDF) de la distribución uniforme discreta se puede expresar, para cualquier k ∈ [ a , b ], como

 ${\displaystyle F(k;a,b)={\frac {\lfloor k\rfloor -a+1}{b-a+1}}}$

DISTRIBUCION GEOMETRICA 

 La distribución geométrica es un modelo adecuado para aquellos procesos en los que se repiten pruebas hasta la consecución del éxito a resultado deseado y tiene interesantes aplicaciones en los muestreos realizados de esta manera . También implica la existencia de una dicotomía de posibles resultados y la independencia de las pruebas entre sí.

Proceso experimental del que se puede hacer derivar

Esta distribución se puede hacer derivar de un proceso experimental puro o de Bernouilli en el que tengamos las siguientes características

· El proceso consta de un número no definido de pruebas o experimentos separados o separables. El proceso concluirá cuando se obtenga por primera vez el resultado deseado (éxito).

· Cada prueba puede dar dos resultados mutuamente excluyentes : A y no A

· La probabilidad de obtener un resultado A en cada prueba es p y la de obtener un resultado no A es q
siendo (p + q = 1).

Las probabilidades p y q son constantes en todas las pruebas ,por tanto , las pruebas ,son independientes (si se trata de un proceso de "extracción" éste se llevará a , cabo con devolución del individuo extraído) .

· (Derivación de la distribución). Si en estas circunstancias aleatorizamos de forma que tomemos como variable aleatoria X = el número de pruebas necesarias para obtener por primera vez un éxito o resultado A , esta variable se distribuirá con una distribución geométrica de parámetro p.

                                                                                           

Obtención de la función de cuantía

    De lo dicho anteriormente , tendremos que la variable X es el número de pruebas necesarias para la consecución del primer éxito. De esta forma la variables aleatoria toma valores enteros a partir del uno ; í 1,2,………ý

    La función de cuantía P(x) hará corresponder a cada valor de X la probabilidad de obtener el primer éxito precisamente en la X-sima prueba. Esto es , P(X) será la probabilidad del suceso obtener X-1 resultados "no A" y un éxito o resultado A en la prueba número X teniendo en cuenta que todas las pruebas son independientes y que conocemos sus probabilidades tendremos:

                          
dado que se trata de sucesos independientes y conocemos las probabilidades

                                             

                                                luego la función de cuantía quedaría 

DISTRIBUCION HIPERGEOMETRICA 

La distribución hipergeométrica es una distribución discreta que modela el número de eventos en una muestra de tamaño fijo cuando usted conoce el número total de elementos en la población de la cual proviene la muestra. Cada elemento de la muestra tiene dos resultados posibles (es un evento o un no evento). Las muestras no tienen reemplazo, por lo que cada elemento de la muestra es diferente. Cuando se elige un elemento de la población, no se puede volver a elegir. Por lo tanto, la probabilidad de que un elemento sea seleccionado aumenta con cada ensayo, presuponiendo que aún no haya sido seleccionado.

Utilice la distribución hipergeométrica para muestras obtenidas de poblaciones relativamente pequeñas, sin reemplazo. Por ejemplo, la distribución hipergeométrica se utiliza en la prueba exacta de Fisher para probar la diferencia entre dos proporciones y en muestreos de aceptación por atributos cuando se toman muestras de un lote aislado de tamaño finito.

La distribución hipergeométrica se define por 3 parámetros: tamaño de la población, conteo de eventos en la población y tamaño de la muestra.

Por ejemplo, usted recibe un envío de pedido especial de 500 etiquetas. Supongamos que el 2% de las etiquetas es defectuoso. El conteo de eventos en la población es de 10 (0.02 * 500). Usted toma una muestra de 40 etiquetas y desea determinar la probabilidad de que haya 3 o más etiquetas defectuosas en esa muestra. La probabilidad de que haya 3 o más etiquetas defectuosas en la muestra es de 0.0384.

DISTRIBUCION POISSON 

Esta distribución es una de las más importantes distribuciones de variable discreta. Sus principales aplicaciones hacen referencia a la modelización de situaciones en las que nos interesa determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de tiempo o de espacio, bajo presupuestos de aleatoriedad y ciertas circunstancias restrictivas. Otro de sus usos frecuentes es la consideración límite de procesos dicotómicos reiterados un gran número de veces si la probabilidad de obtener un éxito es muy pequeña .  

Proceso experimental del que se puede hacer derivar

    Esta distribución se puede hacer derivar de un proceso experimental de observación en el que tengamos las siguientes características

· Se observa la realización de hechos de cierto tipo durante un cierto periodo de tiempo o a lo largo de un espacio de observación

· Los hechos a observar tienen naturaleza aleatoria ; pueden producirse o no de una manera no determinística.

· La probabilidad de que se produzcan un número x de éxitos en un intervalo de amplitud t no depende del origen del intervalo (Aunque, sí de su amplitud)

· La probabilidad de que ocurra un hecho en un intervalo infinitésimo es prácticamente proporcional a la amplitud del intervalo.

· La probabilidad de que se produzcan 2 o más hechos en un intervalo infinitésimo es un infinitésimo de orden superior a dos.

En consecuencia, en un intervalo infinitésimo podrán producirse O ó 1 hecho pero nunca más de uno

· Si en estas circunstancias aleatorizamos de forma que la variable aleatoria X signifique o designe el "número de hechos que se producen en un intervalo de tiempo o de espacio", la variable X se distribuye con una distribución de parámetro l . Así :           

    El parámetro de la distribución es, en principio, el factor de proporcionalidad para la probabilidad de un hecho en un intervalo infinitésimo. Se le suele designar como parámetro de intensidad , aunque más tarde veremos que se corresponde con el número medio de hechos que cabe esperar que se produzcan en un intervalo unitario (media de la distribución); y que también coincide con la varianza de la distribución.

    Por otro lado es evidente que se trata de un modelo discreto y que el campo de variación de la variable será el conjunto de los número naturales, incluido el cero:    

 

Función de cuantía

        A partir de las hipótesis del proceso, se obtiene una ecuación diferencial de definición del mismo que puede integrarse con facilidad para obtener la función de cuantía de la variable "número de hechos que ocurren en un intervalo unitario de tiempo o espacio "

                                                              Que sería :         

DISTRIBUCION BINOMIAL 

La distribución binomial es una distribución de probabilidad discreta que nos dice el porcentaje en que es probable obtener un resultado entre dos posibles al realizar un número n de pruebas.

La probabilidad de cada posibilidad no puede ser más grande que 1 y no puede ser negativa.

En estas pruebas deberemos tener sólo dos resultados posibles, como al lanzar una moneda que salga cara o cruz o en una ruleta francesa que salga rojo o negro.

Cada experimento es independiente de los otros que hagamos y no influye en las probabilidades de los siguientes, en cada uno la probabilidad de que se de uno de los dos resultados será exactamente la misma.

Por ejemplo, si lanzamos un dado la posibilidad de que el resultado sea par (2, 4 ó 6) o impar (1, 3 ó 5) será exactamente la misma si el dado está bien equilibrado, el 50% y por muchas veces que lo lancemos la probabilidad, en cada una de esas veces, seguirá siendo el 50%.

En la distribución binomial tenemos tres variables:

• n es el número de veces que repetimos el experimento.
• p es uno de los dos resultados al que llamaremos éxito.
• q es el otro resultado posible al que llamaremos fracaso.

Como p y q son los dos únicos resultados posibles, entre los dos su porcentaje debe sumar uno por lo que p=1-q.

Para hacer el experimento lo primero que tenemos que hacer es definir p, es decir, en el ejemplo del dado definir si éxito o p es que salga un número par o impar; a partir de ahí, q será la otra posibilidad.

Otro ejemplo: supongamos que vamos con prisa por la calle y queremos tomar un taxi, vamos a calcular la probabilidad de que el próximo taxi que pase esté libre u ocupado. Como hoy está lloviendo es muy probable que esté ocupado. Vamos a asignar a la probabilidad de que esté libre un 15% (es decir, 0,15). Si definimos p o éxito como la probabilidad de que esté libre la de que esté ocupado será q que, al ser 1-p será 1-0,15, es decir 0,85 o, dicho en porcentaje, el 85%

Así, si queremos saber la probabilidad de que un resultado ocurra determinadas veces utilizaremos estos porcentajes.

Por ejemplo, si observamos que pasan diez taxis y queremos saber la probabilidad de que tres de ellos estén libres la fórmula sería:

Donde P es la probabilidad de que tres taxis de los diez estén libres, r las veces que queremos calcular que estén libres, en este caso tres, p el porcentaje de éxito, en este caso 0,15, elevado a r, que hemos visto antes, por q (el porcentaje de fracaso que, en este caso es 0,85) elevado a n menos r; n sobre r se calcula utilizando números factoriales.

DESCRIPCION BINOMIAL NEGATIVO 

 Esta distribución puede considerarse como una extensión o ampliación de la distribución geométrica . La distribución binomial negativa es un modelo adecuado para tratar aquellos procesos en los que se repite un determinado ensayo o prueba hasta conseguir un número determinado de resultados favorables (por vez primera) .Es por tanto de gran utilidad para aquellos muestreos que procedan de esta manera. Si el número de resultados favorables buscados fuera 1 estaríamos en el caso de la distribución geométrica . Está implicada también la existencia de una dicotomía de resultados posibles en cada prueba y la independencia de cada prueba o ensayo, o la reposición de los individuos muestreados.

Proceso experimental del que puede hacerse derivar

Esta distribución o modelo puede hacerse derivar de un proceso experimental puro o de Bernouilli en el que se presenten las siguientes condiciones

· El proceso consta de un número no definido de pruebas separadas o separables . El proceso concluirá cuando se obtenga un determinado número de resultados favorables K

· Cada prueba puede dar dos resultados posibles mutuamente excluyentes A y no A

· La probabilidad de obtener un resultado A en cada una de las pruebas es p siendo la probabilidad de no A , q . Lo que nos lleva a que p+q=1

· Las probabilidades p y q son constantes en todas las pruebas. Todas las pruebas son independientes. Si se trata de un experimento de extracción éste se llevará cabo con devolución del individuo extraído, a no ser que se trate de una población en la que el número de individuos tenga de carácter infinito.

· (Derivación de la distribución) Si, en estas circunstancias aleatorizamos de forma que la variable aleatoria x sea "el número de pruebas necesarias para conseguir K éxitos o resultados A " ; entonces la variable aleatoria x seguirá una distribución binomial negativa con parámetros p y k

                                                                   será entonces    

La variable aleatoria x podrá tomar sólo valores superiores a k 

El suceso del que se trata podría verse como:

                                                    

                   o lo que es lo mismo

                                                 

dado que las pruebas son independientes y conocemos que P(A)= p y P(no A)= q

                                             

que sería la probabilidad de x si el suceso fuera precisamente con los resultados en ese orden. Dado que pueden darse otros órdenes , en concreto  formas u órdenes distintos . La función de cuantía de la distribución binomial negativa quedará como :

                                                      

CONCLUSION; Estas distribuciones son métodos determinados para poder determinar la probabilidad de diferentes eventos. 

Aquí te dejo este video para mejor comprensión: